- Introduction
- Polar form
-
Complex functions
Handy tips included. -
Simple notation
Making complex less painful. - 2D made simple
Anyone can harness complex numbers.
Magic Number loves complex numbers.
It happily takes the square root of –4.
It obviously knows Euler’s identity.
This is the button for imaginary unit.
 ( Shortcut: i )
( Shortcut: i )
It lets you enter complex numbers in the form x + y i.
Or if you prefer, x + i y.
Of course, you can go further than arithmetic.
Complex numbers can be represented in a 2D complex plane.
Earlier, we used the rectangular (Cartesian) form, x + y i.
You can also use the polar form, r ∠ θ.
Here is the polar button.
 ( Shortcut: < )
( Shortcut: < )
Enter 3 ∠ 45, press return, and you get:
By default, Magic Number shows complex result in rectangular form.
To see it in polar, go to menu View ▸ Complex Result ▸ Polar.
In practice, it’s quicker to press ⌥⌘P to switch between rectangular and polar.
These functions are under Calculation ▸ Extra Functions.
In practice, it’s quicker and easier to use or .
When you click them for the first time, you are presented with a list.
(You can also press ⇧⌘F for the list.)

Let’s pick — this gives you the real part of a complex number.
You can click the Examples button to learn more.
Easier shortcuts
F1 and F2 are not easy to press. Besides, they could be used by macOS.
Here are the easier shortcuts:
→ F
→ G
F1 can fit 2 functions
If you look under Calculation ▸ Extra Functions ▸ Complex Numbers, notice how related functions are grouped, e.g., ‘Real Part…’ and ‘Imaginary Part…’

If F1 is ‘Real Part’, to access ‘Imaginary Part’, you press F1 twice.
→ Real Part
→ Imaginary Part
Or if you prefer the easy shortcut:
F → Real Part
F F → Imaginary Part
Of course the same applies to F2.
The versatile ‘part’ function
The part function gives you the real or imaginary part.
For example:
If your complex number is in polar form, you can get the absolute value or the argument.
Polar to rectangular conversions
Earlier you learned that to see the result in polar, you need to switch view by pressing ⌥⌘P.
If you like, you can do so via functions — no need to switch views.
You can convert to polar
and vice versa.
Auto bracketing for , ,
By syntax, these functions come after a complex number, therefore Magic Number can examine what you entered and insert parentheses when necessary.
For examples:
1 + 2i 2
3 ∠ 45
What’s good to know:
Complex numbers have the forms a ± b i, r ∠ θ.
But our workflow and habits vary. For example, a + i b and b i + a are both valid.
Therefore Magic Number takes a less strict approach, it will auto bracket something ± something and something ∠ something.
Give it a try. It saves you time for most cases.
If you prefer to bracket manually, it’s also good to know these tips.
The complex pain
Take the complex number 4 + 5 i.
While it is mathematically descriptive, it can be cumbersome.
If we want to multiply by 3, we cannot just write 3 × 4 + 5 i.
Instead we have to use parentheses and write 3 × (4 + 5 i).
This is because multiplication has higher precedence than addition.
Let’s subtract. Again 3 – 4 + 5 i is no good.
We have to write 3 – (4 + 5 i).
In fact, we need parentheses for division, square root, trigonometry, and almost anything. It’s a parenthesizing pain.
The solution
We can find inspiration nearby.
Let’s look at 4.5. It has 4 as the whole part and 5 as the fractional part.
We use the decimal separator ‘ . ’ to separate the parts. Mathematically, it means 4 + 5/10.
But we rarely write ‘4 + 5/10’. Besides being long, it’s cumbersome for math —
we need parentheses for almost anything, for example:
3 × (4 + 5/10) and 3 – (4 + 5/10).
It’s the same pain. You can see how the decimal separator helps.
For complex numbers, we need a complex separator.
The complex separator
We choose underscore ‘_’ as it is easy to type, distintive, and it doesn’t conflict with math.
Let’s compare the notations.
| x + y i | x_y |
| Standard | Simple |
| 12 + 34 i | 12_34 |
| Standard | Simple |
Let’s compare the math.
| Standard | Simple | |
| Standard | Simple |
Math is not only easier to type, it’s clearer too.
| Standard | Simple | |
| Standard | Simple |
In the next topic, we will exploit simple notation for 2D math.
Simple notation, x_y, makes complex numbers more approachable for 2D math. You can use it to represent width and height.
For example, let’s enlarge a 16 by 9 photo 400%.
To calculate the new dimension, we need to do the same math twice:
16 × 4 and 9 × 4.
Now we can simply use 16 _ 9 to represent 16 by 9.
Enter: 16 _ 9 × 4.
To see the result in simple notation, go to menu
View ▸ Complex Result ▸ Notation ▸ x _ y
2D variable
Let’s say you shoot videos in 4k (3840 by 2160) and you often need resolutions for various scales.
As we use this master resolution a lot, let’s set it to m.
Enter: m = 3840 _ 2160
What’s the resolution at 50%?
Let’s make it 4 times smaller.
Distance between 2 points
What is the distance between (7, 5) and (3, 2)?
Enter: 7 _ 5 – 3 _ 2
Not quite the result as it is the horizontal and vertical distances.
We want the direct distance as shown by the blue line.
We can use Pythagorean theorem.
But it’s quicker to see the result in polar coordinates.
(Which in effect gives you the length and the angle of the blue line.)
To switch to polar view, press ⌥⌘P
The distance is 5.
Scalar product
As 2D is based on complex numbers, Magic Number uses the star symbol ( * ) for scalar multiplication. To get it, press multiply twice, that is, .
To calculate (1, 2) • (3, 4), enter 1 _ 2 ×× 3 _ 4.
Angle between 2 vectors
The polar operator can help — it has an extra trick up its sleeve.
( shortcut: < ).
Generally, it is used to specify complex number in polar format, in the form of
radius ∠ angle. Of course, radius and angle have to be real to make sense.
But when either side is complex, they will be treated as vectors and Magic Number will calculate the angle between them.
For example, to calculate the angle between (1, 2) and (3, 4),
enter (1, 2) ∠ (3, 4).
Storing 2D numbers
2D-List is an ideal place for 2D numbers.
Here is a 2D number.
To store it, open 2D-List (⌘5) and press ↩
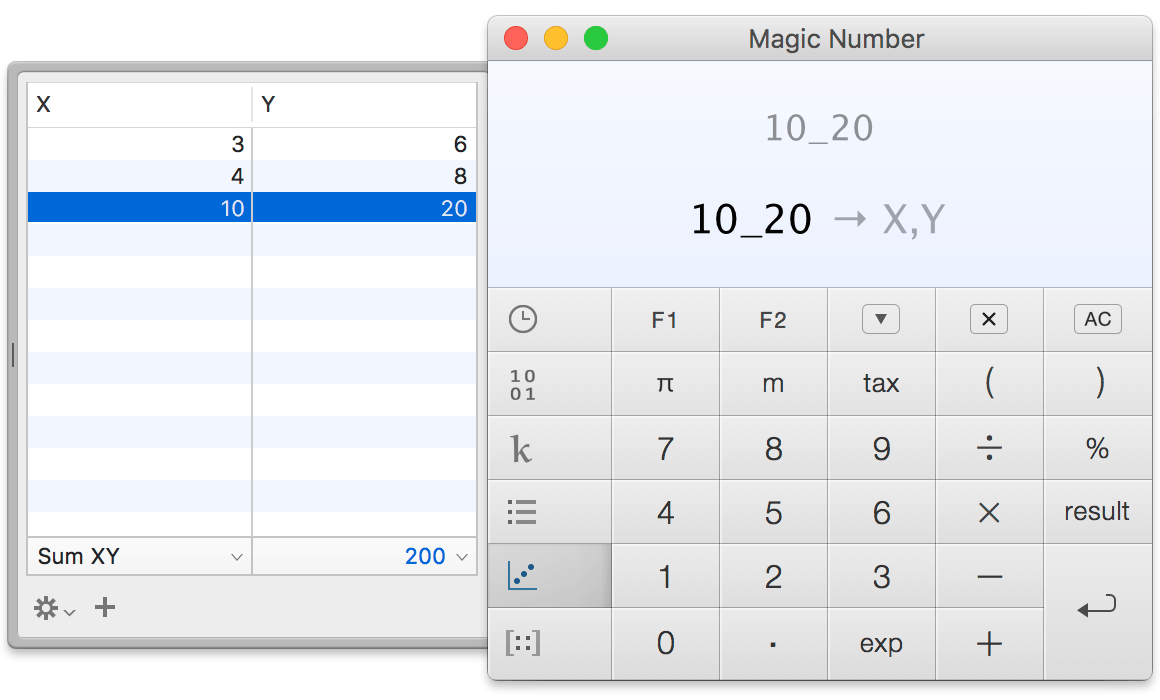
What’s good to know:
- Notice the parts are splitted and stored under X and Y.
This gives you more flexibility. For example, you can sort by X. - Right-click (secondary click) a number on the list, you get a menu
where you can choose what to insert. - The function Sum XY.
If you use X for width and Y for height, then XY is the area.
The screenshot shows the area of a selected row.
Another non-2D use: X as the quantity and Y as the price.